A four-headed cat state

Author: Guillaume Thekkadath

In this tutorial, we numerically simulate the protocol proposed in Engineering Schrödinger cat states with a photonic even-parity detector, Quantum 4, 239 (2020), for engineering superpositions of coherent states. In particular we look at how to make a coherent superposition of four coherent states, a four-headed cat state.

import numpy as np
from qutip import wigner, Qobj, wigner_cmap

import matplotlib.pyplot as plt
import matplotlib as mpl
from matplotlib import cm

import strawberryfields as sf
from strawberryfields.ops import *
from thewalrus.quantum import state_vector, density_matrix

Ideal preparation

Here we setup some basic parameters, like the value of the photon-number-resolving detectors we will use to herald and the parameters of the different Gaussian unitaries.

Lambda = 0.999 # As explained in the paper, the four-component cat state scheme works less well for finite squeezing.
r = np.arctanh(Lambda)
fourCatSize = 14 # One obtains a better fidelity when this number is an integer (see paper for explanation)
# As per scheme, we first prepare a two-component cat state with half the size of the desired four-component cat
twoCatSize = fourCatSize / 2
alpha = np.sqrt(twoCatSize)
nModes = 5
nMax = 30
detOutcome1 = int(round(twoCatSize))
detOutcome2 = int(round(fourCatSize))
print(detOutcome1,detOutcome2)

7 14

Now we setup a 3-mode quantum circuit in Strawberry Fields and obtain the covariance matrix and vector of means of the Gaussian state.

nmodes = 5
prog = sf.Program(nmodes)
eng = sf.Engine("gaussian")
with prog.context as q:
    Dgate(1j*alpha)|q[0]
    S2gate(r)|(q[1],q[2])
    BSgate()|(q[0],q[1])
    Dgate(1j*alpha)|q[2]
    S2gate(r)|(q[3],q[4])
    BSgate()|(q[2],q[3])
state = eng.run(prog).state
mu = state.means()
cov = state.cov()

# Here we use the sf circuit drawer and standard linux utilities
# to generate an svg representing the circuit
file, _ = prog.draw_circuit()
filepdf = file[0:-3]+"pdf"
filepdf = filepdf.replace("circuit_tex/","")
filecrop = filepdf.replace(".pdf","-crop.pdf")
name = "four_cat_circuit.svg"
!pdflatex  $file > /dev/null 2>&1
!pdfcrop $filepdf > /dev/null 2>&1
!pdf2svg $filecrop $name

Here is a graphical representation of the circuit. It is always assumed that the input is vacuum in all the modes.

We can now inspect the covariance matrix and vector of means. Note that the vector of means is non-zero since we used a displacement gate.

np.set_printoptions(linewidth=120)
print(np.round(mu,3))
print(np.round(cov,3))

[0.    0.    0.    0.    0.    3.742 3.742 3.742 3.742 0.   ]
[[ 500.25  -499.25  -499.75  -499.75     0.       0.      -0.       0.       0.       0.   ]
 [-499.25   500.25   499.75   499.75     0.      -0.       0.      -0.      -0.       0.   ]
 [-499.75   499.75   999.5      0.    -706.753    0.      -0.       0.      -0.       0.   ]
 [-499.75   499.75     0.     999.5    706.753    0.      -0.      -0.       0.      -0.   ]
 [   0.       0.    -706.753  706.753  999.5      0.       0.       0.      -0.       0.   ]
 [   0.      -0.       0.       0.       0.     500.25  -499.25   499.75   499.75     0.   ]
 [  -0.       0.      -0.      -0.       0.    -499.25   500.25  -499.75  -499.75     0.   ]
 [   0.      -0.       0.      -0.       0.     499.75  -499.75   999.5     -0.     706.753]
 [   0.      -0.      -0.       0.      -0.     499.75  -499.75    -0.     999.5   -706.753]
 [   0.       0.       0.      -0.       0.       0.       0.     706.753 -706.753  999.5  ]]

We now use the walrus to obtain the Fock representation of the heralded state when modes 0 and 1 are heralded in the value \(n=7\) and modes 2 and 3 are heralded in the value \(n=14\). This information is stored in the variable psi. We also calculate the probability of success in heralding in the variable p_psi.

psi = state_vector(mu, cov, post_select={0:detOutcome1, 1:detOutcome1, 2:detOutcome2, 3:detOutcome2},
                   normalize=False, cutoff=nMax)
p_psi = np.linalg.norm(psi)
psi = psi / p_psi
print("The probability of successful heralding is ", np.round(p_psi**2,10))

The probability of successful heralding is  4e-09

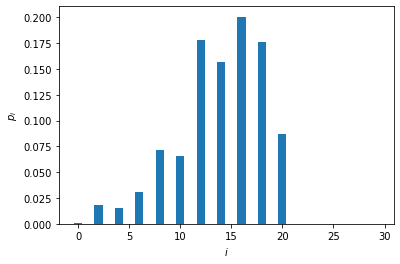
We now plot the photon-number distribution of the heralded state. Note that the state only has even photon components.

plt.bar(np.arange(nMax),np.abs(psi)**2)
plt.xlabel("$i$")
plt.ylabel(r"$p_i$")
plt.show()

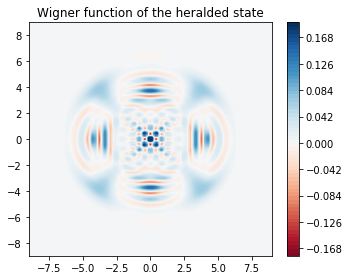
We can now plot the Wigner function of the heralded state,

grid = 100
xvec = np.linspace(-9,9,grid)
Wp = wigner(Qobj(psi), xvec, xvec)
wmap = wigner_cmap(Wp)
sc1 = np.max(Wp)
nrm = mpl.colors.Normalize(-sc1, sc1)
fig, axes = plt.subplots(1, 1, figsize=(5, 4))
plt1 = axes.contourf(xvec, xvec, Wp, 60,  cmap=cm.RdBu, norm=nrm)
axes.contour(xvec, xvec, Wp, 60,  cmap=cm.RdBu, norm=nrm)
axes.set_title("Wigner function of the heralded state");
cb1 = fig.colorbar(plt1, ax=axes)
fig.tight_layout()
plt.show()

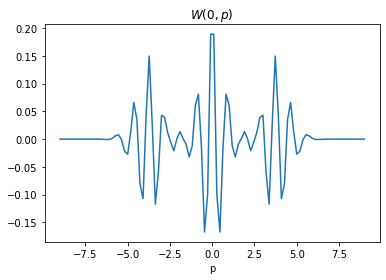
and a cut of the Wigner function along \(p=0\).

plt.plot(xvec, Wp[:,grid//2])
plt.title(r"$W(0,p)$")
plt.xlabel(r"p")
plt.show()

%reload_ext version_information
%version_information qutip, strawberryfields, thewalrus

Software	Version
Python	3.7.5 64bit [GCC 7.3.0]
IPython	7.10.1
OS	Linux 4.15.0 72 generic x86_64 with debian stretch sid
qutip	4.4.1
strawberryfields	0.13.0-dev
thewalrus	0.11.0-dev
Mon Dec 30 10:17:05 2019 EST

Note

Click here to download this gallery page as an interactive Jupyter notebook.

gallery/four_cat

 

Download Python script

 

Download Notebook

 

View on GitHub